Probability of Submarine Cable Cuts in the Baltic Sea

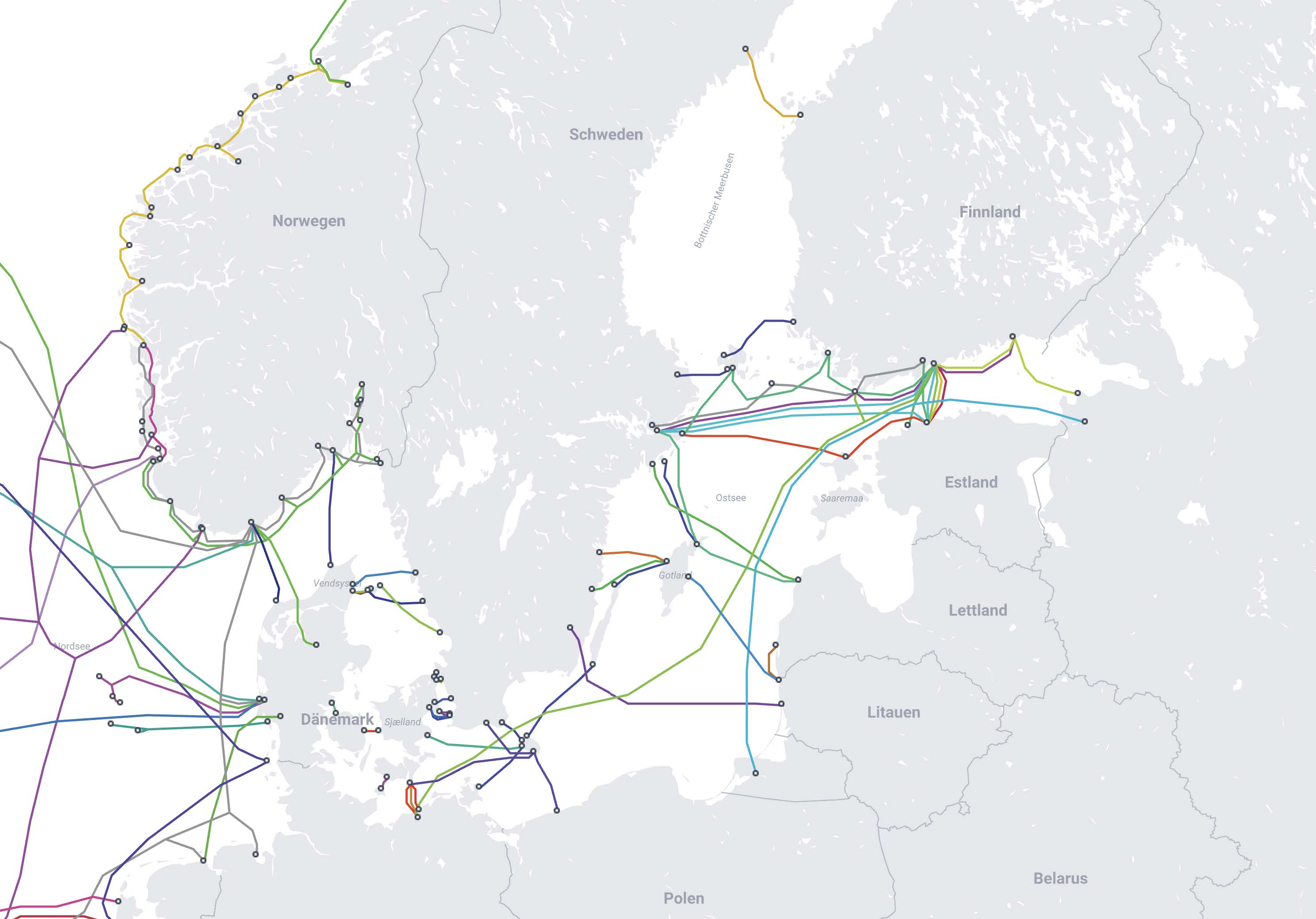
An analysis of submarine cable disruptions in the Baltic Sea using statistical models.

1. Introduction

Knowing that 200 undersea cables break every year globally, we estimate the probability of:

• A single cable break in the Baltic Sea on a given day.
• Three cable breaks in the Baltic Sea on the same day.

These estimates are based on global statistics and reasonable approximations.

2. Average Daily Cable Breaks Globally

• Total global undersea cable breaks per year: 200.
• Number of days in a year: $365$.
• Average breaks per day globally:

$\frac{200}{365} \approx 0.548 \, \text{breaks/day}$

3. Estimating Cable Breaks in the Baltic Sea

• Assuming the Baltic Sea contains about $1\%$ of the world’s undersea cables:

$\text{Expected breaks/year in the Baltic Sea: } \allowbreak 0.01 \times 200 = 2 \, \text{breaks/year}.$

• Average breaks per day in the Baltic Sea:

$\frac{2}{365} \approx 0.00548 \, \text{breaks/day}.$

4. Using the Poisson Distribution

Since cable breaks are rare and occur independently, we use the Poisson distribution with rate $\lambda = 0.00548$ (average number of daily breaks in the Baltic Sea).

The probability mass function is:

$P(k; \lambda) = \frac{e^{-\lambda} \lambda^k}{k!}$

where $k$ is the number of events.

4.1 Probability of a Single Cable Break ($k = 1$)

For $k = 1$ and $\lambda = 0.00548$:

$P(1; 0.00548) = \frac{e^{-0.00548} \cdot 0.00548^1}{1!}$

Steps:

• $e^{-0.00548} \approx 1 - 0.00548 = 0.99452$.
• $P(1; 0.00548) = 0.99452 \cdot 0.00548 \approx 0.00545$.

Thus, the probability of a single break is approximately:

$P(1; 0.00548) \approx 0.00545 \, (\text{or about } 0.545\%).$

4.2 Probability of Three Cable Breaks ($k = 3$)

For $k = 3$ and $\lambda = 0.00548$:

$P(3; 0.00548) = \frac{e^{-0.00548} \cdot 0.00548^3}{3!}$

Steps:

• $e^{-0.00548} \approx 0.99452$.
• $0.00548^3 \approx 1.64566 \times 10^{-7}$.
• $3! = 6$.
• $P(3; 0.00548) = \frac{0.99452 \cdot (1.64566 \times 10^{-7})}{6} \allowbreak \approx 2.73 \times 10^{-8}$.

Thus, the probability of three breaks is approximately:

$P(3; 0.00548) \approx 2.73 \times 10^{-8}.$

Conclusion

• The probability of a single cable break in the Baltic Sea on a given day is approximately:

$P(1; 0.00548) = ~0.545\%.$

• The probability of three cable breaks in the Baltic Sea on the same day is about:

$P(3; ~0.00548) ~\approx~2.73~\times~10^{-8}~\allowbreak (\text{or approximately }~1~\text{in }~36~\text{million}).$